Самое актуальное и обсуждаемое
Популярное
Полезные советы
Важно знать!
9 способов определить местоположение iphone
Как найти iPhone с компьютера?
Предположим, что вы потеряли iPhone и никак не можете его найти самостоятельно. Используя персональный компьютер с подключением к сети Интернет и веб-интерфейс iCloud решить...
Читать далее
11 способов создания загрузочной флешки и записи iso-образа для windows 10
3 приложения для накрутки подписчиков в тик ток
7 способов справиться с хейтерами в социальных сетях
10 сайтов, которые помогут создать крутой логотип
3d моделирование в современном мире
10 лучших видеопроигрывателей для windows (от xp до 10-ки)
4 способа поделиться интернетом на мтс с одного телефона на другой
10 лучших машинок для удаления катышек
17track — китайский сервис отслеживания почтовых отправлений
Лучшее
Важно знать!
10 лучших бесплатных программ для записи видео с экрана: рейтинг 2020 года
Скриншотер
Скриншотер — одна из самых простых и малоразмерных программ для записи видео и игр с экрана ПК. Это бесплатное приложение от отечественных разработчиков позволяет в пару кликов мышью не только...
Читать далее
7 способов узнать какая видеокарта стоит на компьютере
14 лучших бюджетных смартфонов
50+ лучших сайтов для заработка денег
6 способов отключения узла службы локальной системы, грузящей диск windows 10
3 простых способа удалить звук из видео в windows 10
7 лучших утилит для восстановления удалённых данных
100 вдохновляющих вопросов, которые заставят вас задуматься о своей жизни
5 online word art generator websites free
5 простых советов, как составить инвестиционный портфель новичку
Новое
Обсуждаемое

Важно знать!
10 лучших программ для рисования на компьютере
MyPaint
Программа предназначена в большей степени для художников, работающих в классических жанрах. Она не столько разработана под рисование простых иллюстраций, сколько под создание художественных произведений,...
Читать далее
5 курортов россии, где уже в мае отлично подогрето море
7 лучших фитнес браслетов с пульсометром и давлением
27 бесплатных и лучших приложений для android на 2021 год
29 сервисов виртуальных номеров для приема смс
25 бесплатных онлайн-курсов по веб-дизайну [2021]
33 захватывающих фильма о смысле жизни
2 этапа запуска восстановления системы виндовс 10 через командную строку
7 лучших книг по инвестированию
0xc000007b
Популярное
Актуальное

Важно знать!
121 название для беседы в вк
советы и примеры удачных названий
Как назвать группу в WhatsApp?
Название виртуального сообщества должно цеплять пользователей. Придумывая ему имя, необходимо учитывать следующие факторы:
Тема общения....
Читать далее
12 лучших игровых смартфонов
0x0000007e
10 отличных инструментов, для подбора правильного сочетания шрифтов
9 микропривычек, которые за год изменят вашу жизнь
30 лучших курсов по дизайну с нуля
25 идей для нового хобби и 50 ресурсов-помощников
21 книга о том, как построить гармоничные отношения с окружающими
18 лучших графических редакторов, которые не стоят ни копейки
10 простых способов разблокировки графического пароля
Обновления
 Статьи
Как начать инвестировать в криптовалюты: руководство для новичков
Статьи
Как начать инвестировать в криптовалюты: руководство для новичков
Криптовалюты стали одним из самых горячих тем в мире финансовых инвестиций и электронных платежей....
 Статьи
Продвижение бренда в соцсетях: эффективные стратегии для онлайн-успеха
Статьи
Продвижение бренда в соцсетях: эффективные стратегии для онлайн-успеха
7 эффективных стратегий продвижения бренда в социальных сетях: советы и секреты успешного привлечения...
 Статьи
Lineage 2: MMORPG — обзор и нюансы в многопользовательской онлайн-игре!
Статьи
Lineage 2: MMORPG — обзор и нюансы в многопользовательской онлайн-игре!
Выбрть высокорейтовый сервер – это значит, что шанс выпадения опыта и предметов повышен. Это делает...
 Статьи
Плюсы и минусы windows 11
Статьи
Плюсы и минусы windows 11
Активация операционной системы является важной процедурой, которая обеспечивает ее легальное использование...
 12 рабочих способов как скачать музыку с вк на компьютер бесплатно
12 рабочих способов как скачать музыку с вк на компьютер бесплатно
Качаем музыку на флешку
Подключите флешку к ПК и убедитесь, что в средстве «Компьютер» она распознаётся...
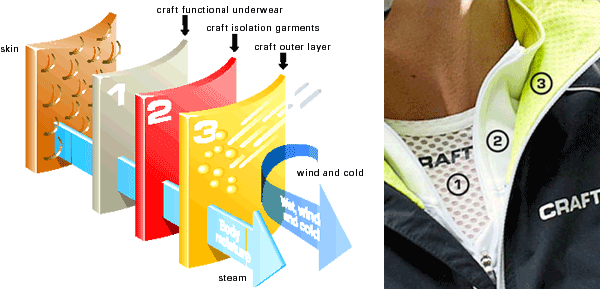 20 лучших брендов термобелья для взрослых и детей
20 лучших брендов термобелья для взрослых и детей
Лучшие производители мужского термобелья
Мужское термобелье из шерсти многослойно, поскольку создается...
 6 способов отключения адаптивной регулировки автояркости в ос windows 10
6 способов отключения адаптивной регулировки автояркости в ос windows 10
Как отрегулировать яркость экрана компьютера, автоматически и вручную
Часто возникает надобность увеличить...
 5 лучших приложений для фотопечати 2020 года
5 лучших приложений для фотопечати 2020 года
Создаем фото 3×4 онлайн
Под редактированием снимка рассматриваемого размера чаще всего подразумевается...
 7 трюков для работы в word, о которых знает далеко не каждый
7 трюков для работы в word, о которых знает далеко не каждый
Поиск по словам и фразам через панель «Навигация»
Чтобы найти какую-либо фразу или слово в документе...
 8 лучших блокировщиков рекламы
8 лучших блокировщиков рекламы
Как заблокировать рекламу на YouTube с помощью AdLock?
AdLock считается лучшим блокировщиком рекламы,...
 6 причин, почему смартфон быстро разряжается
6 причин, почему смартфон быстро разряжается
Особенности использования
Батарея смартфона быстрее разряжается при интернет-серфинге, просмотре фильмов,...
 11 главных вопросов, которые нужно задать работодателю на собеседовании
11 главных вопросов, которые нужно задать работодателю на собеседовании
Вопросы о должности и о самой работе:
1. Какие мои должностные обязанности? Первое, что вы стараетесь...